Homework8

Homework 8

Reading and prepping data

library(ggplot2) # for graphics
library(MASS) # for maximum likelihood estimation
library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ lubridate 1.9.4     ✔ tibble    3.2.1
## ✔ purrr     1.0.2     ✔ tidyr     1.3.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ✖ dplyr::select() masks MASS::select()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

z <- read.table("Homework8Data.csv", header=TRUE, sep=",")
z <- select(z, Rainfall)
z <- data.frame(1:597, z)
names(z) <- list("ID","myVar")
z <- z[z$myVar>0,]
str(z)

## 'data.frame':    597 obs. of  2 variables:
##  $ ID   : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ myVar: num  9.14 7.14 13.39 9.17 3.38 ...

summary(z$myVar)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   0.080   4.830   7.820   9.937  12.290  54.460

Packages were loaded in to allow for ggplot and tidyverse commands. Z was assigned the data table, and it was modified to only include the values from the “Rainfall” column using select(). A data frame of two columns, “ID” and “myVar” (the rainfall data), was then made using data.frame() and names().

Plot histogram

p1 <- ggplot(data=z, aes(x=myVar, y=..density..)) +
  geom_histogram(color="grey60",fill="cornsilk",size=0.2) 
print(p1)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.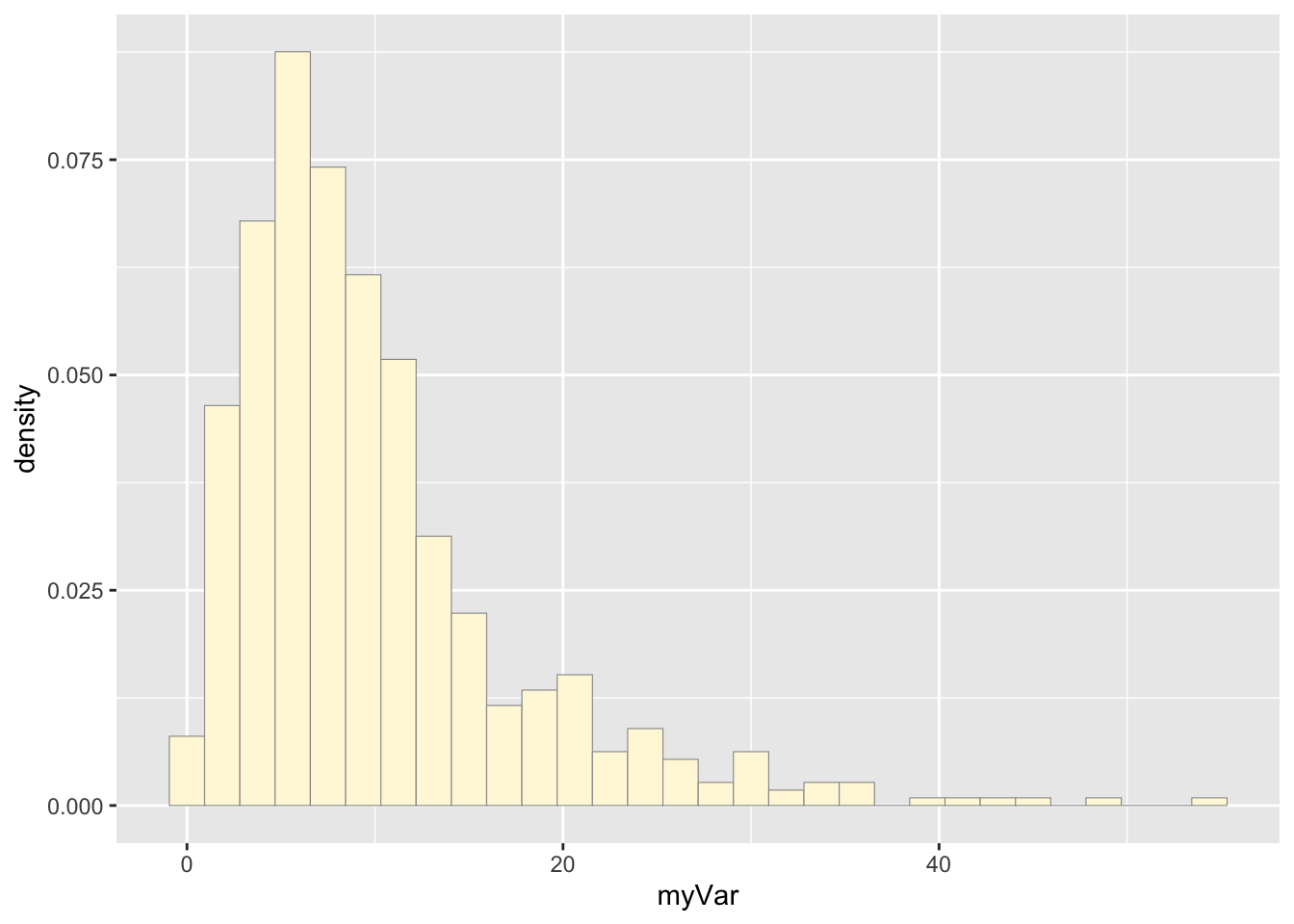

The variable p1 was assigned a histogram using the “myVar” data from data frame z. “myVar” values were the x values which were plotted against their density (y).

Add empirical density curve

p1 <-  p1 +  geom_density(linetype="dotted",size=0.75)
print(p1)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.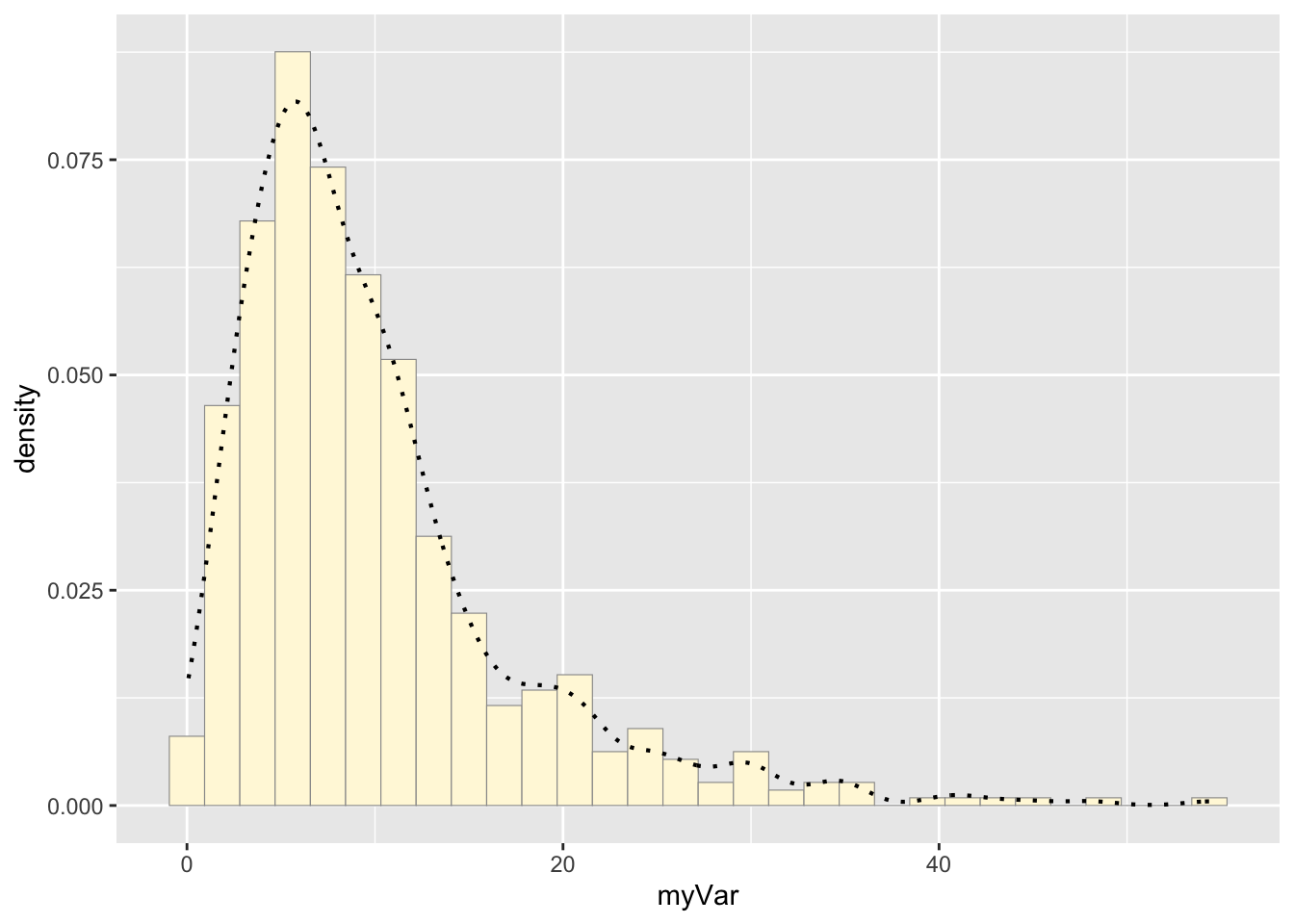

An empirical density line was added to the histogram plot by assigning p1 to equal p1 + the density curve line (made with geom_density)

Get maximum likelihood parameters for normal

normPars <- fitdistr(z$myVar,"normal")
print(normPars)

##      mean         sd    
##   9.9371357   7.6544595 
##  (0.3132762) (0.2215197)

str(normPars)

## List of 5
##  $ estimate: Named num [1:2] 9.94 7.65
##   ..- attr(*, "names")= chr [1:2] "mean" "sd"
##  $ sd      : Named num [1:2] 0.313 0.222
##   ..- attr(*, "names")= chr [1:2] "mean" "sd"
##  $ vcov    : num [1:2, 1:2] 0.0981 0 0 0.0491
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:2] "mean" "sd"
##   .. ..$ : chr [1:2] "mean" "sd"
##  $ n       : int 597
##  $ loglik  : num -2062
##  - attr(*, "class")= chr "fitdistr"

normPars$estimate["mean"] # note structure of getting a named attribute

##     mean 
## 9.937136

The function fitdistr() found the mean and standard deviation of the data following a normal probability distribution. This data, a list of 5, was stored in the variable normPars. The mean was isolated with normPars$estimate["mean']: the variable was called for, the list item was specified with $, and the mean was found by matching its name.

Plot normal probability density

meanML <- normPars$estimate["mean"]
sdML <- normPars$estimate["sd"]
xval <- seq(0,max(z$myVar),len=length(z$myVar))

stat <- stat_function(aes(x = xval, y = ..y..), fun = dnorm, colour="red", n = length(z$myVar), args = list(mean = meanML, sd = sdML))
p1 + stat

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.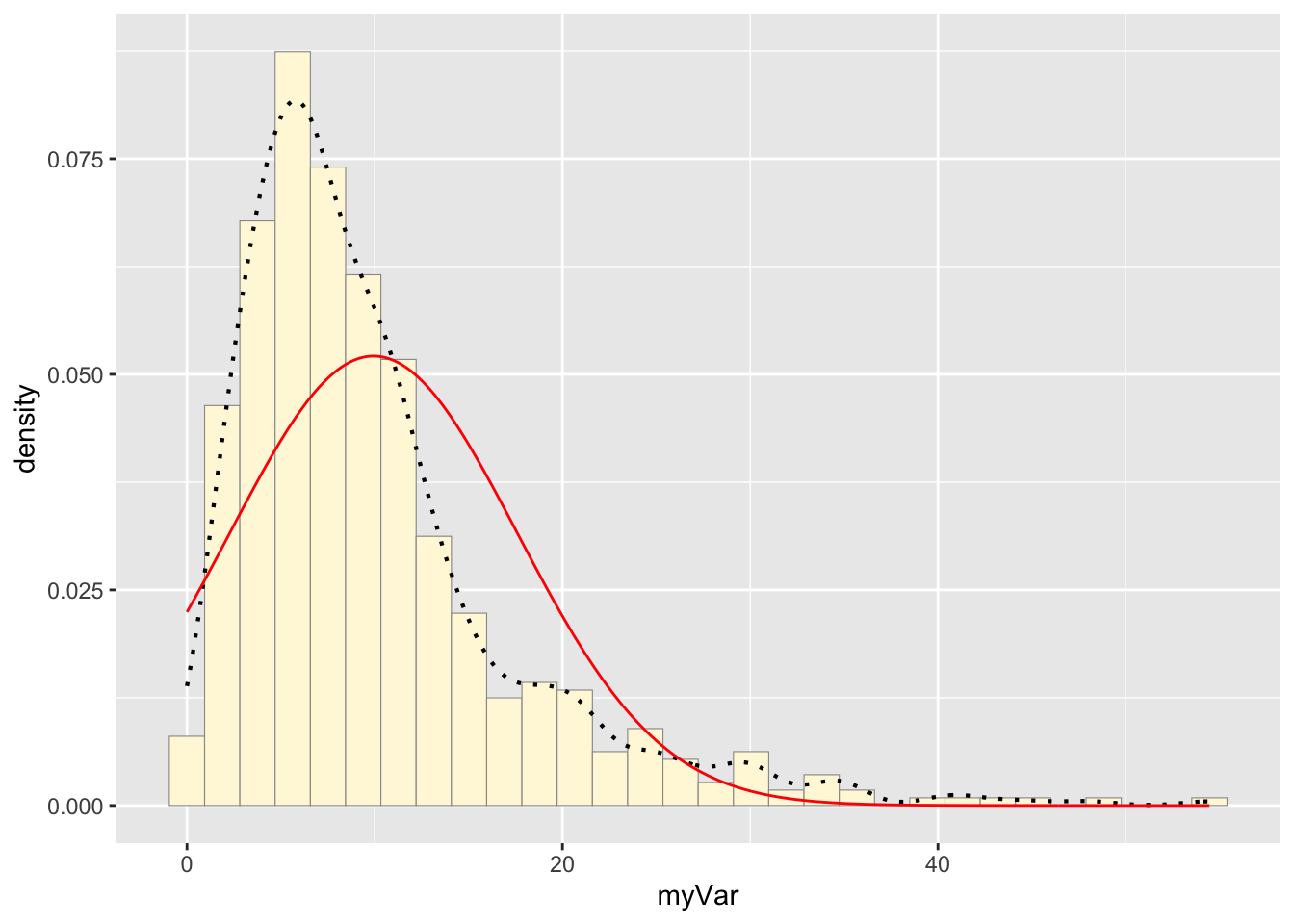

The variable stat was assigned a dnorm function that created a normal probability density curve based on the mean and standard deviation held in normPars. The curve was then added to the histogram with p1 + stat.

Plot exponential probability density

expoPars <- fitdistr(z$myVar,"exponential")
rateML <- expoPars$estimate["rate"]

stat2 <- stat_function(aes(x = xval, y = ..y..), fun = dexp, colour="blue", n = length(z$myVar), args = list(rate=rateML))
p1 + stat + stat2

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.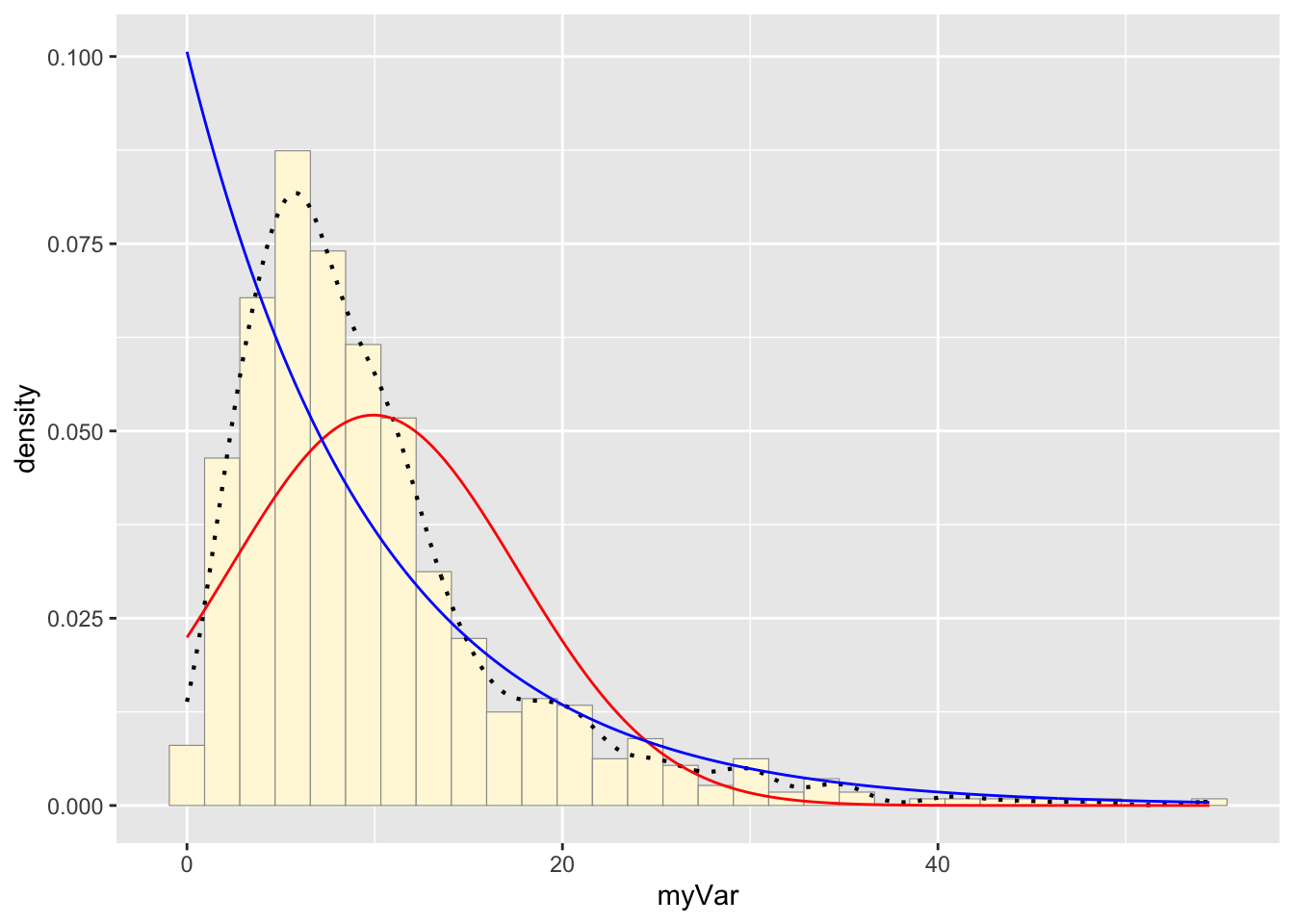

fitdistr() was used to fit the data to the exponential density model. The variable stat1 was then assigned a dexp function that created an exponential probability density curve based on the rate found by fitdistr(). The new curve was added to the histogram.

Plot uniform probability density

stat3 <- stat_function(aes(x = xval, y = ..y..), fun = dunif, colour="darkgreen", n = length(z$myVar), args = list(min=min(z$myVar), max=max(z$myVar)))
p1 + stat + stat2 + stat3

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.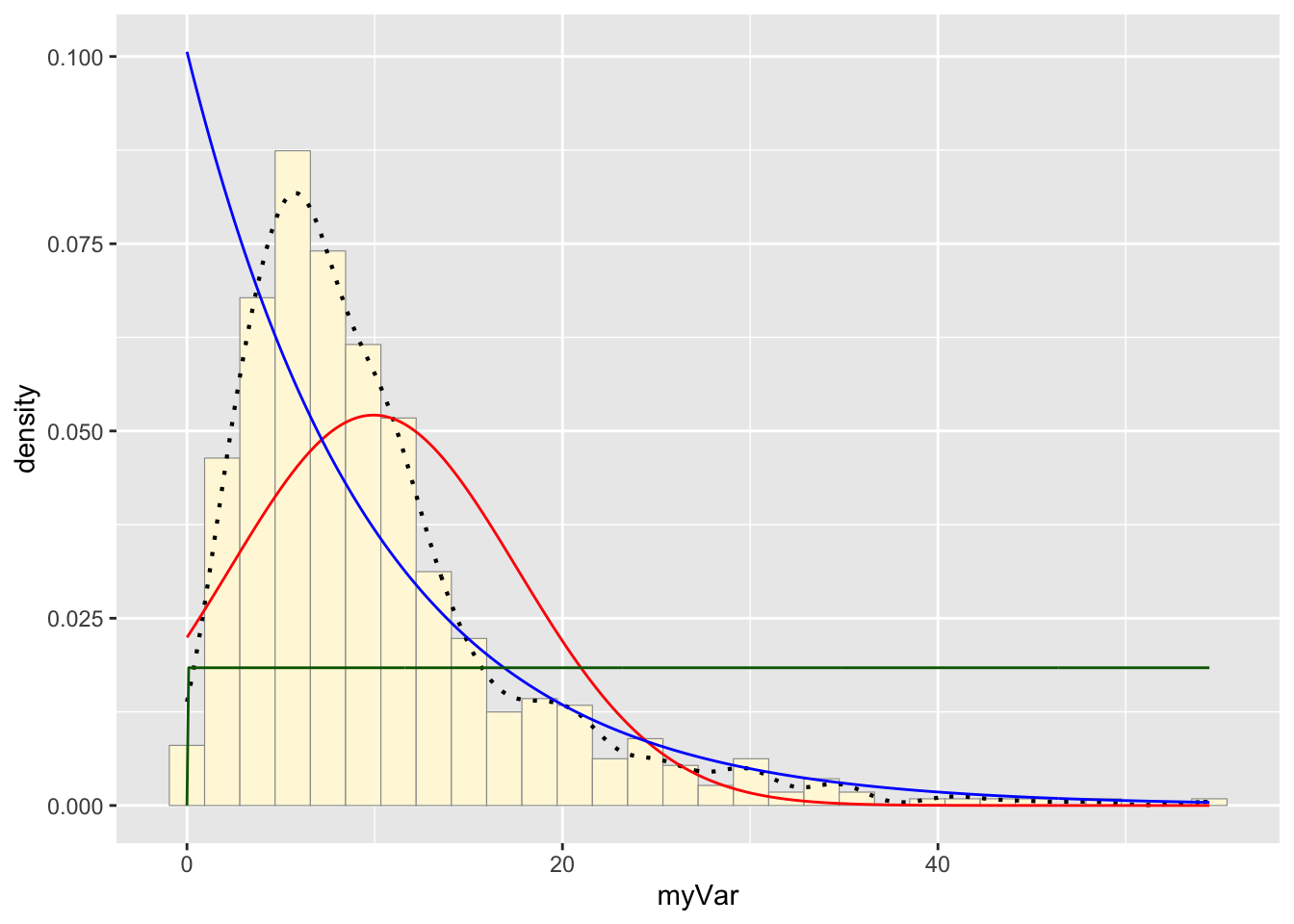

The variable stat3 was assigned a dunif function that created a uniform probability density curve based on the maximum and minimum values of “myVar”. The curve generated was added to the histogram.

Plot gamma probability density

gammaPars <- fitdistr(z$myVar,"gamma")
shapeML <- gammaPars$estimate["shape"]
rateML <- gammaPars$estimate["rate"]

stat4 <- stat_function(aes(x = xval, y = ..y..), fun = dgamma, colour="brown", n = length(z$myVar), args = list(shape=shapeML, rate=rateML))
p1 + stat + stat2 + stat3 + stat4

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.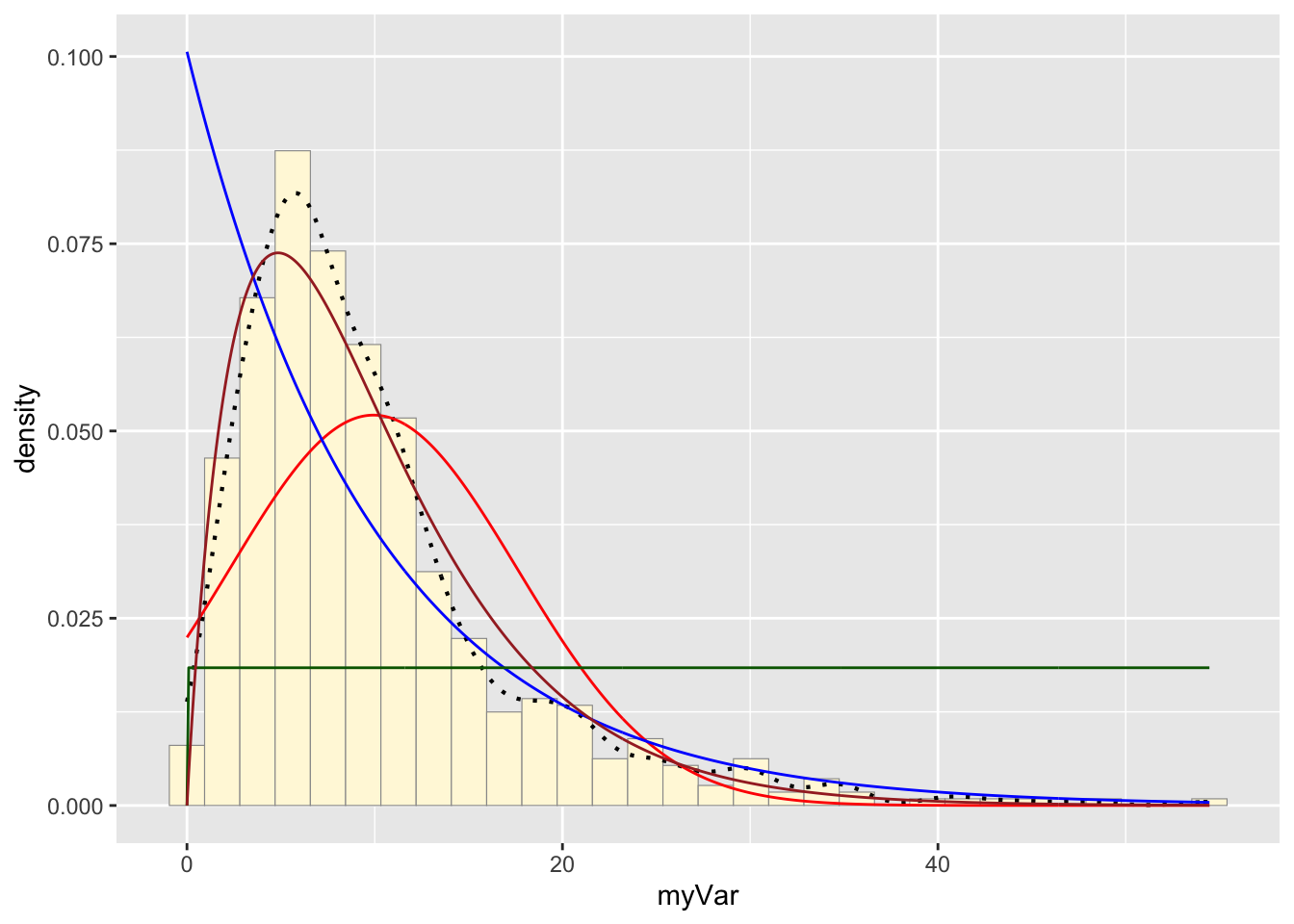

The function fitdistr() found the shape and rate of the data following a gamma probability distribution. This data was stored in the variable gammaPars. The variable stat4 was assigned a dgamma function that created a gamma probability density curve based on the rate and shape found in gammaPars. The curve generated was added to the histogram.

Plot beta probability density

pSpecial <- ggplot(data=z, aes(x=myVar/(max(myVar + 0.1)), y=..density..)) +
  geom_histogram(color="grey60",fill="cornsilk",size=0.2) + 
  xlim(c(0,1)) +
  geom_density(size=0.75,linetype="dotted")

betaPars <- fitdistr(x=z$myVar/max(z$myVar + 0.1),start=list(shape1=1,shape2=2),"beta")
shape1ML <- betaPars$estimate["shape1"]
shape2ML <- betaPars$estimate["shape2"]

statSpecial <- stat_function(aes(x = xval, y = ..y..), fun = dbeta, colour="orchid", n = length(z$myVar), args = list(shape1=shape1ML,shape2=shape2ML))
pSpecial + statSpecial

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.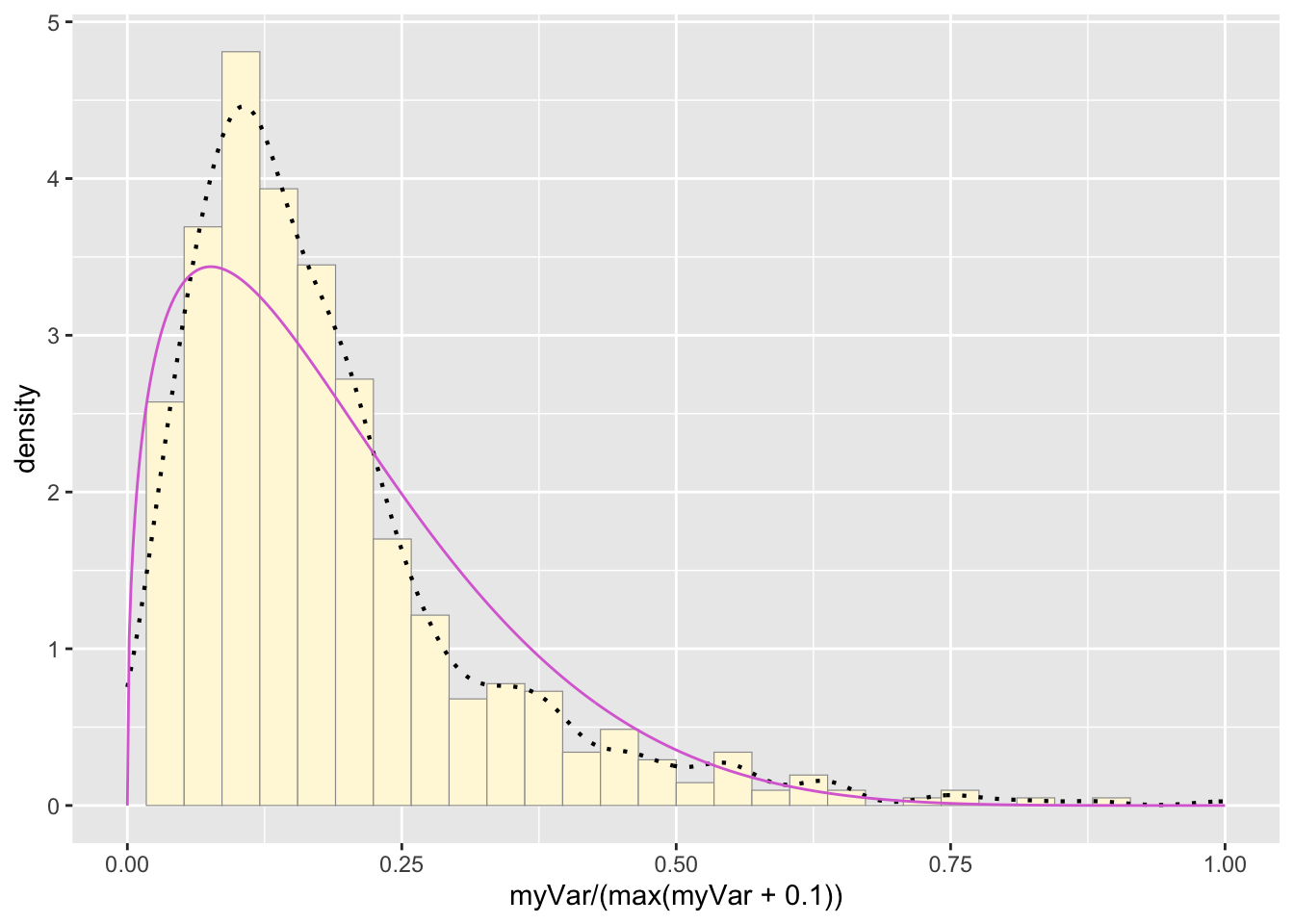

A new histogram was made to accommodate the differing x value parameters of a beta probability density curve. The new histogram, pSpecial, plotted the density of the “myVar” values on a scale of 0 to 1 by dividing each value by 0.1 more than the maximum value of the dataset. These values were also used to fit the data to a beta probability density distribution. The two shapes found by the fitdistr() function were used to make a beta probability density curve that was added to the new histogram.

The data’s fit

The data best fit the gamma probability density model.

Simulating new dataset

y <- rgamma(597, 1.95, rate=0.197)
y <- data.frame(1:597, y)
names(y) <- list ("ID", "myVar")
y <- y[y$myVar>0,]

py <- ggplot(data=y, aes(x=myVar, y=..density..)) +
  geom_histogram(color="grey60",fill="cornsilk",size=0.2) 
print(py + stat4)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.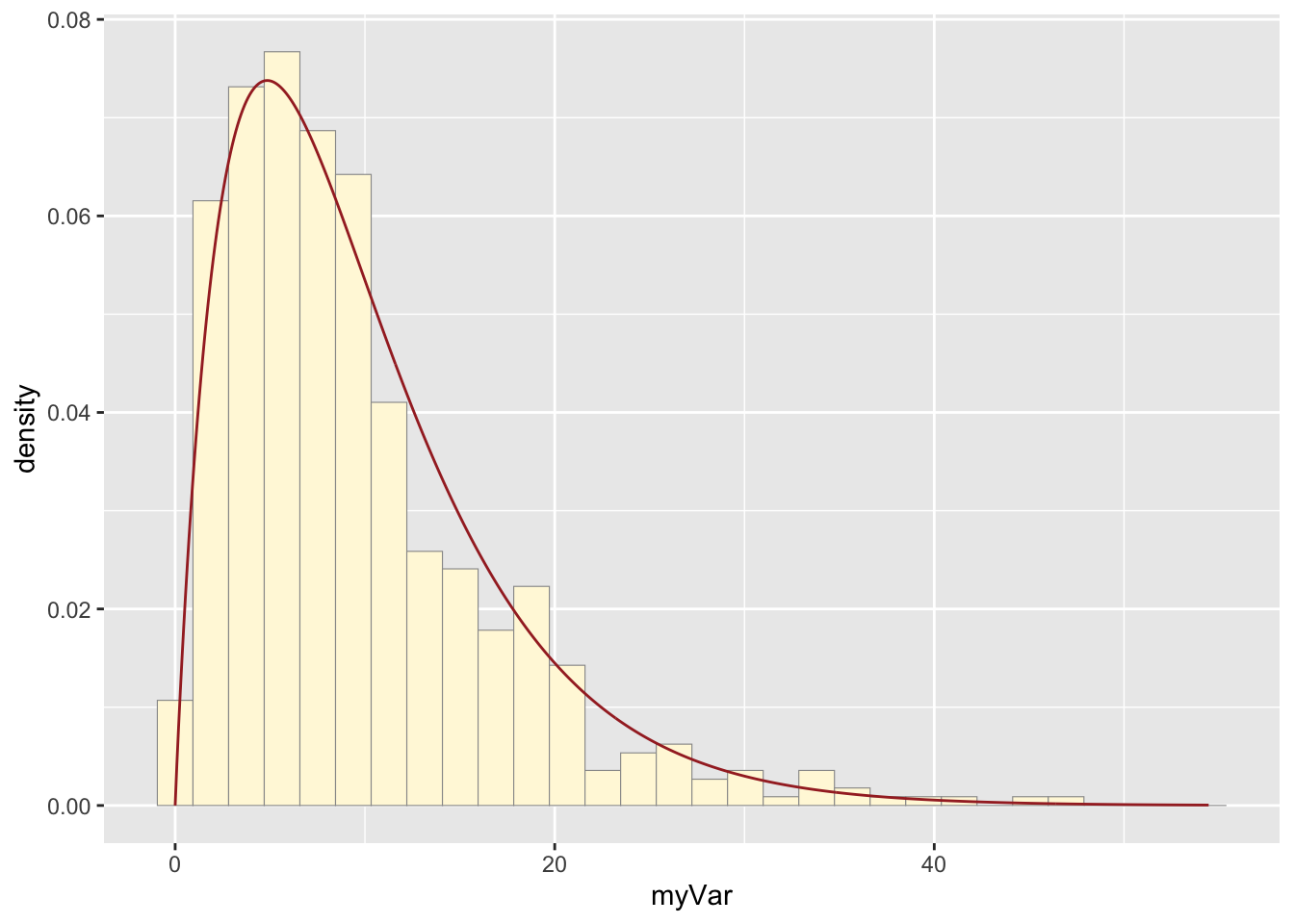

print(p1 + stat4)

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.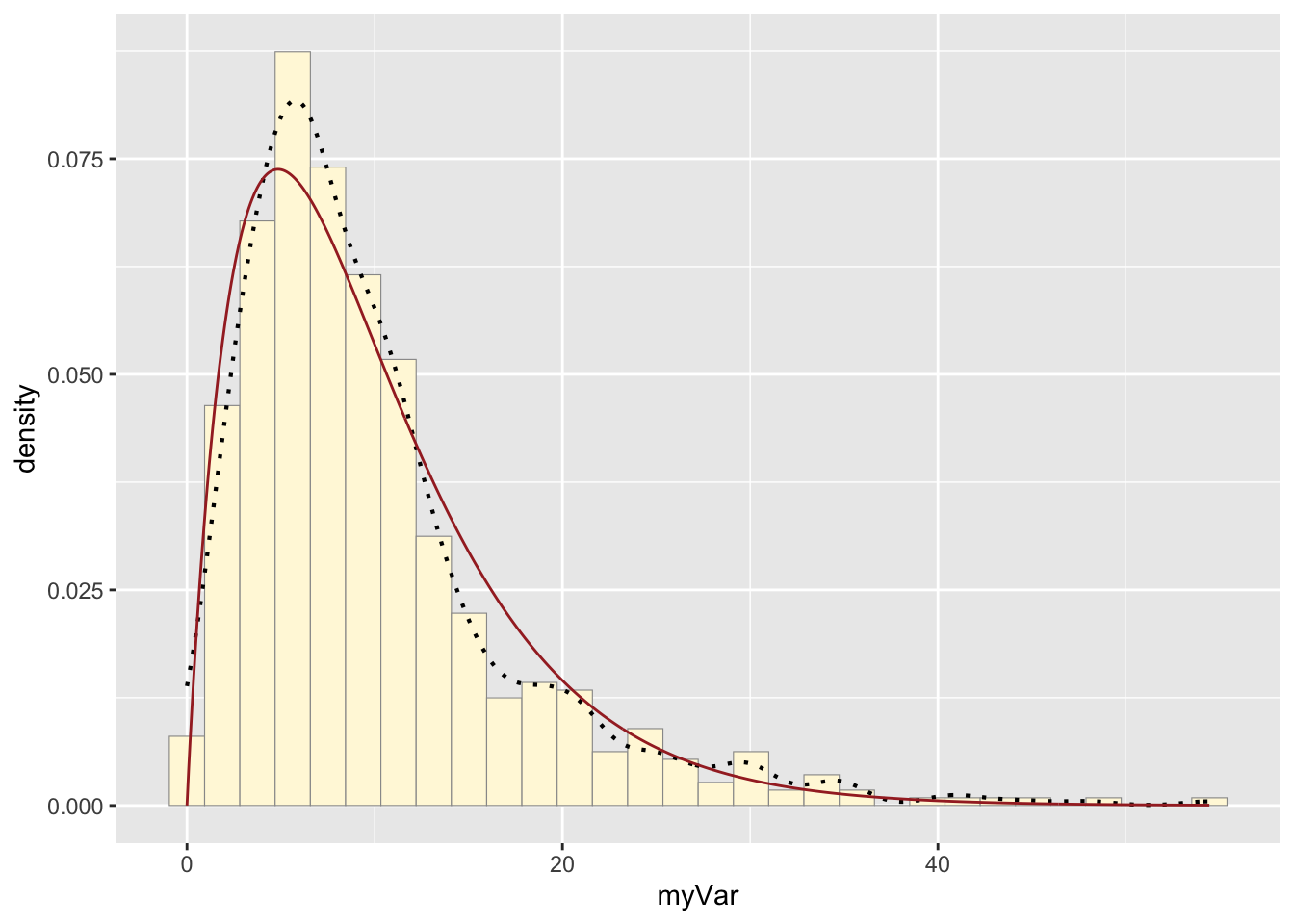

A new vector of values, y, was made by using rgamma() to generate data that fit the gamma model and had the same parameters (shape and rate) as the origional dataset, z. The vector was made into a data frame with the values now under the name “myVar”. A new plot, py, generated a historgram of the new values. The gamma distribution curve made before was printed with the new histogram, and the origional histogram was also printed with the same gamma distribution curve. The histograms look fairly similar: they have very similar shapes, but the origional data reaches a higher maximum. While the model was mostly realistic, it did not fully capture the density of the most popular x values.